Monday, 28 September 2020

Write your own Integer to String (itoa) implementation in Java

Write your own Integer to String (itoa) converter.

Implement your own Integer to ASCII (itoa) method which converts an Integer to String.

Input 1: 123
Output: "123" (as String)

Input 2: 0
Output: "0" (as String)

Input 3: 8
Output: "8" (as String)

Algorithm

Before we look into the algorithm, lets understand the ASCII ranges for 0-9.

ASCII  Char 
--------------- 
 48   0    
 49   1    
 50   2    
 51   3    
 52   4    
 53   5    
 54   6    
 55   7    
 56   8    
 57   9 

so if we have integer 4 and we want to get the char representation of 4, we can get by
char number = '0' + 4 which would be 48 + 4 = 52 and when we do ((char) 52) we get '4'.

similarly, if we have integer 7 and we want to get the char representation of 7, we can get by
char number = '0' + 7 which would be 48 + 7 = 55 and when we do ((char) 55) we get '7'.

Lets jump to original problem, if given the number 123

Mod and Divide the number by 10 to read each digits from end, once we have the digit convert it in the way shown below and put in StringBuilder.

Java Program to convert Integer To Ascii.

package javabypatel;

public class IntegerToASCII {
    public static void main(String[] args) {
        System.out.println(integerToAscii(10));
    }

    private static String integerToAscii(int num) {
        StringBuilder sb = new StringBuilder();
        while (num > 0) {
            int lastDigit = num % 10;
            char ch = (char) ('0' + lastDigit);

            // since we are processing the last digit first(reverse order),
            // inserting at 0th position so that output is not in reverse order.
            sb.insert(0, ch);
            num /= 10;
        }
        return sb.toString();
    }
}
at No comments:

Write your own String to Integer (atoi) implementation in Java

Write your own String to Integer (atoi) converter.

Implement your own ASCII to Integer (atoi) method which converts a string to an integer.

Input 1: "123"
Output: 123 (as int)

Input 2: "0"
Output: 0 (as int)

Input 3: "8"
Output: 8 (as int)

Algorithm

Before we look into the algorithm, lets understand the ASCII ranges for 0-9.

ASCII  Char 
--------------- 
 48   0    
 49   1    
 50   2    
 51   3    
 52   4    
 53   5    
 54   6    
 55   7    
 56   8    
 57   9 

so if we have char '4' and we want to get the Integer representation of '4', we can get by

int number = '4' - '0' which would be 52 - 48 = 4 (an integer 4), 

similarly, if we want to get the integer representation of char '7', just subtract it by '0'.
int number = '7' - '0' which would be 55 - 48 = 7 (an integer 7), similarly

Lets jump to original problem, if given the String "123"

Iterate the String, get the first character '1', convert it to Integer as shown above.
Similarly for all the characters of the String.

For getting the integer number, we will use the technique, 

sum = 0 initially.
sum = (sum * 10) + (str.charAt(i) - '0') 

Java Program to convert Ascii To Integer.

    

package javabypatel;

public class ASCIIToInteger {
    public static void main(String[] args) {
        System.out.println(asciiToInt("10"));
    }

    private static int asciiToInt(String num) {
        int result = 0;
        for (int i = 0; i < num.length(); i++) {
            char ch = num.charAt(i);
            result = (result * 10) + (ch - '0');
        }
        return result;
    }
}
at No comments:

Sunday, 27 September 2020

Merge all overlapping intervals in Java

Merge overlapping intervals in Java.

Given a N pairs of intervals. merge all overlapping intervals..

You are given a pair of intervals in a format (start time, end time), Merge intervals that overlaps with each other.

Consider this problem as asking someone availability in their calendar, and if the person calendar is like below,
Meeting from [[1,2],[2,3],[3,4],[10,12]] what the person will say?
I am busy from [1-4] and [10-12], it is like merging intervals that overlaps.

Example of Merging overlapping intervals

merge overlapping intervals

Let see some more input and output:

Example 1: Input: intervals = [[1,2],[2,3],[3,4],[10,15]]
Output: [[1,4],[10,15]]

Example 2: Input: intervals = [[1,5],[3,5],[2,6],[10,15]]
Output: [[1,6],[10,15]]

Example 3: Input: intervals = [[1,4],[2,6]]
Output: [[1,6]]

Algorithm

Lets say we are given below time intervals

(1, 4), (7, 9), (3, 6), (8, 10)

If we sort the time intervals based on start time,

(1, 4), (3, 6), (7, 9), (8, 10)

If we see the first two interval, end time of first interval is greater than start time of second interval which means there is overlap of (end time - start time).

Our task is to Iterate all the intervals and compare, if there is overlap, just Merge the both intervals into one and expand the endInterval window by comparing endTime of both intervals and consider the one which is highest.

(1, 4), (3, 6), 

Merged Interval = (1, 6)

(7, 9)

totally new range, doesn't overlap with the Merged Interval till now (1, 6)

Put it in our Merged Interval list [(1, 6), (7, 9)] 

(8, 10)

Compare the top interval from merged interval list that is compare (7, 9) with (8, 10)

there is overlap, update the window (7, 10), update the merged interval list (1, 6) (7, 10).

Java Program to Merge overlapping intervals.

    
package javabypatel

import java.util.Arrays;
import java.util.Collections;
import java.util.List;
import java.util.Stack;

public class MergeOverlappingIntervals {

    public static void main(String[] args) {
        List<Interval> intervals = Arrays.asList(
                new Interval(1, 2),
                new Interval(2, 3),
                new Interval(3, 4),
                new Interval(10, 15));

        Stack<Interval> mergedIntervals = new MergeOverlappingIntervals().mergeOverlappingIntervals(intervals);
        System.out.println(mergedIntervals);
    }

    public Stack<Interval> mergeOverlappingIntervals(List<Interval> intervals) {
        if (intervals == null) {
            return null;
        }

        Stack<Interval> stack = new Stack<>();
        if (intervals.size() < 2) {
            stack.addAll(intervals);
            return stack;
        }

        Collections.sort(intervals);

        //We can take any data structure which can help us compare the top element.
        stack.add(intervals.get(0));

        for (int i = 1; i < intervals.size(); i++) {
            Interval nextInterval = intervals.get(i);
            Interval resultInterval = stack.peek();

            //Check if Interval overlaps? If yes, increase the end time
            //example (1, 3) (2, 6) -> Intervals overlaps,
            //end time will be max of both end time = 6
            //since the array is sorted by startTime, no need to update the startTime as smallest will be at top.
            if (resultInterval.endTime >= nextInterval.startTime) {
                //update the peek endTime
                resultInterval.endTime = Math.max(resultInterval.endTime, nextInterval.endTime);
            } else {
                //if no overlaps then this is the new range, add it in stack.
                stack.add(nextInterval);
            }
        }

        return stack;
    }
}
Interval.java 
package javabypatel;

public class Interval implements Comparable<Interval>{
    public int startTime;
    public int endTime;

    public Interval(int startTime, int endTime) {
        this.startTime = startTime;
        this.endTime = endTime;
    }

    @Override
    public int compareTo(Interval interval) {
        if (startTime < interval.startTime) {
            return -1;
        } else if (startTime == endTime) {
            return 0;
        } else {
            return 1;
        }
    }

    @Override
    public String toString() {
        return "Interval{" +
                "startTime=" + startTime +
                ", endTime=" + endTime +
                '}';
    }
}
at No comments:

Saturday, 26 September 2020

Find overlapping interval among a given set of intervals.

Find overlapping interval among a given set of intervals.

Given a N pairs of intervals. Identify interval that overlap with other interval.

You are given a pair of intervals in a format (start time, end time), find interval that overlaps with other interval.

Example of overlapping intervals

find overlapping time intervals

Let see some more input and output:

Example 1:
Input: (1, 3) (3, 5) (5, 7)
Output: No overlapping Intervals.

Example 2: (2, 3) (3, 5) (1, 6)
Output: (1, 6) overlaps with (2, 3)
Though (3, 5) also overlaps with (1, 6) we are mainly looking for one of them. Given solution below find one of them. 

Algorithm

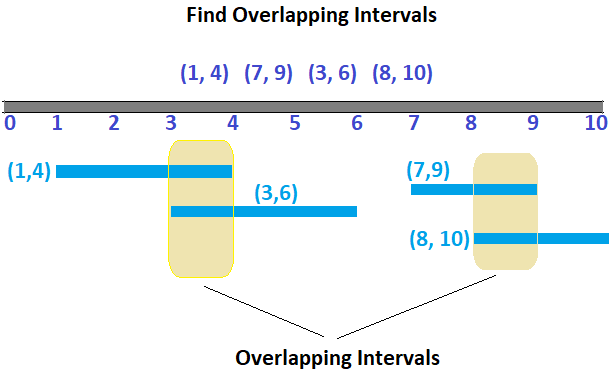
Lets say we are given below time intervals

(1, 4), (7, 9), (3, 6), (8, 10)

If we sort the time intervals based on start time,

(1, 4), (3, 6), (7, 9), (8, 10)

If we see the first two interval, end time of first interval is greater than start time of second interval which means there is overlap of (end time - start time) in this case it is (4 - 3) = overlap of 1 unit.

Our task is to just find the overlapping intervals.

Java Program to find overlapping intervals among a given set of intervals.

package javabypatel;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;

public class OverlappingIntervals {
    public static void main(String[] args) {
        List<Interval> intervals = Arrays.asList(
                new Interval(1, 3),
                new Interval(6, 8),
                new Interval(2, 4),
                new Interval(5, 6));
        List<Interval> interval = new OverlappingIntervals().findOverlappingIntervalApproach1(intervals);
        System.out.println("Overlapping intervals :" + interval);

        boolean isOverlappingIntervals = findOverlappingIntervalApproach2(intervals);
        System.out.println("Is overlapping intervals :" + isOverlappingIntervals);
    }

    //Sort the intervals by start time and compare the endtime of first interval with the start time of next interval.
    //If the endTime of first interval is > then startTime of next interval means there is overlap
    //Example: [(1, 3) (2, 4)]
    //time complexity: (n log n) + n = (n log n)
    public List<Interval> findOverlappingIntervalApproach1(List<Interval> intervals) {
        Collections.sort(intervals); //(n log n)
        List<Interval> overlappingInterval = new ArrayList<>();

        for (int i = 0; i < intervals.size()-1; i++) { //n
            if (intervals.get(i).endTime > intervals.get(i+1).startTime) {
                overlappingInterval.add(intervals.get(i));
                overlappingInterval.add(intervals.get(i+1));
            }
        }
        return overlappingInterval;
    }

    //Another approach which just says there is overlap or not.
    //time complexity:
    // O(n) = to find the max element in array
    // O(m) = where m is the max element in array
    // Total = O(m + n)
    // this approach works well when the range is small
    public static boolean findOverlappingIntervalApproach2(List<Interval> intervals){
        //find the highest end time within list of all intervals
        int highestTime = intervals.get(0).endTime;
        for (int i = 1; i<intervals.size(); i++) {
            int endTime = intervals.get(i).endTime;
            if(highestTime < endTime)
                highestTime = endTime;
        }

        int[] count = new int[highestTime + 1];
        //Mark the count[startTime] to +1 and count[endTime] to -1
        for (int i = 0; i<intervals.size(); i++) {
            Interval current = intervals.get(i);
            count[current.startTime]++;
            count[current.endTime]--;
        }

        //Iterate count array and sum the values
        //if at any point sum is > 1 that means interval overlaps.
        boolean isOverlappingIntervals = false;

        int sum = 0;
        for (int i = 0; i <count.length; i++) {
            sum += count[i];
            if(sum > 1){
                isOverlappingIntervals = true;
                break;
            }
        }

        return isOverlappingIntervals;
    }
}
Interval.java 
package javabypatel;

public class Interval implements Comparable<Interval>{
    public int startTime;
    public int endTime;

    public Interval(int startTime, int endTime) {
        this.startTime = startTime;
        this.endTime = endTime;
    }

    @Override
    public int compareTo(Interval interval) {
        if (startTime < interval.startTime) {
            return -1;
        } else if (startTime == endTime) {
            return 0;
        } else {
            return 1;
        }
    }

    @Override
    public String toString() {
        return "Interval{" +
                "startTime=" + startTime +
                ", endTime=" + endTime +
                '}';
    }
}
Approach 2

In this approach, we are going to take a count array and for each given interval start time we will do count[startTime]++ and for end time, do count[endTime]--.

After filling the count array, iterate count array and do the sum of counts, If at any given index we find 
sum > 2 it means there is overlapping intervals. 

How this approach is working? say if we have intervals as (1, 3) and (2, 5), and count array for this will be. array size will be 5(highest end time in given intervals)
(1, 3) = [0, 1, 0, -1, 0,  0]
(2, 5) = [0, 1, 1, -1, 0, -1]

Whenever we see adjacent one's, it means there is y interval(in this case (2,5)) which has starting time before the end of x interval(1,3).
 
at No comments:

Serialize and Deserialize N-ary tree in Java

Serialize and Deserialize N-ary tree in java

This is a popular interview question asked in Tier-1 companies.

Given an n-ary tree, serialize and deserialize it.

Example of N-ary tree Serialization-Deserialization.

Serialize and Deserialize N-ary Tree

Algorithm

Serialization and Deserialization of N-ary tree is very similar to Serialization and Deserialization of Binary tree.

I would recommend to visit the Serialization/Deserialization post if not visited before: Serialize and Deserialize a Binary Tree

In Binary tree since there are only 2 child, we can get where is the start and end of the child of a particular Node from the serailized key, but in N-ary tree a Node can have n children, so we need some method to identify the start and end of a child nodes.

In this approach we will do a preorder traversal of N-ary tree and place the length of child nodes next to Node value as shown in example below,
 
serialize and deserialize n-ary tree implementation


In Deserialization process, it is exactly reverse now, we know first key in the String is the actual node and next key is the length of child nodes of a key.

Java Program to Serialize Deserialize N-ary tree

package javabypatel;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;

public class SerializeDeserializeNAryTree {

    public static void main(String[] args) {
        NAryNode root = new NAryNode(1,
                Arrays.asList(
                        new NAryNode(2, Arrays.asList(
                                new NAryNode(5),
                                new NAryNode(6),
                                new NAryNode(7, Arrays.asList(
                                        new NAryNode(11),
                                        new NAryNode(12))))),
                        new NAryNode(3),
                        new NAryNode(4, Arrays.asList(
                                new NAryNode(8),
                                new NAryNode(9),
                                new NAryNode(10)))
                ));

        String str = serializeTree(root, new StringBuilder());
        System.out.println(str);
        NAryNode deserializeRoot1 = deserializeApproach1(str == null? null : str.split(","), new int[1]);
        NAryNode deserializeRoot2 = deserializeApproach2(str);

        System.out.println(deserializeRoot1);
        System.out.println(deserializeRoot2);
    }

    //In this approach, we need to take a separate index array of size 1 to remember the next element in array to pick
    //or we can take a static integer to remember the state.
    private static NAryNode deserializeApproach1(String[] arr, int[] index) {
        if (arr == null || index[0] >= arr.length || arr[index[0]] == null) {
            return null;
        }

        NAryNode n = new NAryNode(Integer.parseInt(arr[index[0]++]));
        int size = Integer.parseInt(arr[index[0]++]);
        n.child = new ArrayList<>(size);

        for (int i = 0; i < size; i++) {
            n.child.add(deserializeApproach1(arr, index));
        }
        return n;
    }

    //In this approach, we are converting serialized tree to Queue, so that when we do
    //queue.poll it will remove the element and we don't need to keep track of the next element to process.
    private static NAryNode deserializeApproach2(String str) {
        if (str == null) {
            return null;
        }
        return deserializeHelper(new LinkedList<String>(Arrays.asList(str.split(","))));
    }

    private static NAryNode deserializeHelper(Queue<String> queue) {
        if (queue.isEmpty()) {
            return null;
        }

        NAryNode n = new NAryNode(Integer.parseInt(queue.poll()));
        int size = Integer.parseInt(queue.poll());
        n.child = new ArrayList<>(size);

        for (int i = 0; i < size; i++) {
            n.child.add(deserializeHelper(queue));
        }
        return n;
    }

    private static String serializeTree(NAryNode root, StringBuilder sb) {
        if (root == null) {
            return null;
        }

        sb.append(root.data);
        sb.append(",");

        if (root.child != null) {
            sb.append(root.child.size());
            sb.append(",");
            for (int i = 0; i<root.child.size(); i++) {
                serializeTree(root.child.get(i), sb);
            }
        } else {
            sb.append(0);
            sb.append(",");
        }
        return sb.toString();
    }
}
NAryNode.java
package javabypatel;

import java.util.List;

public class NAryNode {
    public int data;
    public List<NAryNode> child;

    public NAryNode(int data, List<NAryNode> child) {
        this.data = data;
        this.child = child;
    }
    public NAryNode(int data) {
        this.data = data;
    }
}
at No comments:

N-ary tree preorder traversal in java

N-ary tree preorder traversal in java

This is a popular interview question asked in Tier-1 companies.

Given an n-ary tree, print preorder traversal of its nodes values.

Example of N-ary tree preorder traversal below:

n-ary tree preorder traversal example

Algorithm

Preorder traversal: To traverse a Binary Tree in Preorder, following operations are carried-out 
  1. Visit the root node and print data of that node. 
  2. Traverse the left subtree, and 
  3. Traverse the right subtree.

Preorder traversal of N-ary tree is very similar to that of Binary tree preorder traversal, only difference is instead of two children in Binary tree here we have N children.

Preorder traversal of Binary tree: Binary Tree Preorder Traversal

Considering the example above, 
we will first visit the root Node 1, then instead of directly going Left and then Right that is what we do in Binary tree preorder traversal because there is only 2 children, here we don't know the number of child, so what we are going to do is loop for all the child and then do a Preorder traversal for each child.
 
Visit Root Node 1, 
loop for all the children [Node 2, Node 3, Node 4]  (i = 0, i<3; i++) i=0

Visit Node 2, 
Iterate all its children [Node 5, Node 6, Node 7]  (i = 0, i<3; i++) i=0

Visit Node 5,
Iterate all its children []

Node 5 has no children so we came back to Node 2, now i = 1

Came back to Node 2, 
Iterate all its children [Node 5, Node 6, Node 7], (i = 0, i<3; i++), i =2 do for Node 6. 

and it continues.

Java Program to print N-ary tree preorder traversal

package javabypatel;

import java.util.Arrays;

public class NAryTreeTraversal {
    public static void main(String[] args) {
        NAryNode root = new NAryNode(1,
                Arrays.asList(
                        new NAryNode(2, Arrays.asList(
                                    new NAryNode(5),
                                    new NAryNode(6),
                                    new NAryNode(7, Arrays.asList(
                                                new NAryNode(11),
                                                new NAryNode(12))))),
                        new NAryNode(3),
                        new NAryNode(4, Arrays.asList(
                                    new NAryNode(8),
                                    new NAryNode(9),
                                    new NAryNode(10)))
                ));

        preOrderTraversal(root);
    }

    private static void preOrderTraversal(NAryNode start) {
        if (start == null) {
            return;
        }

        System.out.print(start.data + ",");
        if (start.child != null) {
            for (int i = 0; i < start.child.size(); i++) {
                preOrderTraversal(start.child.get(i));
            }
        }
    }
}
NAryNode.java
package javabypatel;

import java.util.List;

public class NAryNode {
    public int data;
    public List<NAryNode> child;

    public NAryNode(int data, List<NAryNode> child) {
        this.data = data;
        this.child = child;
    }
    public NAryNode(int data) {
        this.data = data;
    }
}
at No comments:

Wednesday, 16 September 2020

Minimum deletions required to make frequency of each letter unique in a String in Java

Minimum deletions to make frequency of each character unique

This is a popular interview question asked in Tier-1 companies.

Given a string, find the minimum number of characters to be deleted in a string so that the frequency of each character in the string is unique.

Question 1:
String s = 'aaaabbbcccdddd'
Frequency of characters : { a=4, b=3, c=3, d=4 }

a nd d both have same frequency 4, similarly b and c have same frequency 3. so frequency is repeated and we need to make it unique.
we need to delete three character from a, one characters from b to make their frequency different.
s = 'abbcccdddd'

Frequency of characters : { a=1, b=2, c=3, d=4 }

Detailed Description:
we need to make the frequency unique,
Either we need to delete one character from a or d so that we break the same frequency.
so we delete a, now string is "aaabbbcccdddd"

Now the frequency of a is 3, b is 3, c is 3 and d is 4
the frequency of a, b and c is repeating, we need to delete one character from a,
s = 'aabbbcccdddd'

Now the frequency of a is 2, b is 3, c is 3 and d is 4
the frequency of b and c is repeating, we need to delete one character from b, but this will make b count to 2 which will be same as a count, so we will delete 2 characters from b so the frequency will be 1.
s = 'aabcccdddd'

Now the frequency of a is 2, b is 1, c is 3 and d is 4, so is unique now.

Answer is 4 because we delete 4 characters to make the frequency unique.

Java Program to find minimum deletions in a String to make the frequency of each character unique

package javabypatel;

import java.util.Collections;
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;

public class MinimumDeletionUsingPriorityQueue {
    public static void main(String[] args) {
        System.out.println(countFrequency("aaaabbbcccdddd"));
    }

    private static int countFrequency(String str) {

        if (str == null || str.length() < 2) {
            return 0;
        }

        //Taking a map to find unique occurrence of each character in a string.
        Map<Character, Integer> frequencyCount = new HashMap<>();
        for (char ch: str.toCharArray()) {
            int count = frequencyCount.getOrDefault(ch, 0);
            frequencyCount.put(ch, count + 1);
        }

        //Taking a PriorityQueue for processing the count of each occurrence of a character
        //Putting the values in reverse order so that higher counts are at head
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(Collections.reverseOrder());

        //dumping the frequency of each characters in a Priority queue.
        for (Map.Entry<Character, Integer> entry : frequencyCount.entrySet()) {
            priorityQueue.add(entry.getValue());
        }

        int deletionCount = 0;

        while (!priorityQueue.isEmpty()) {
            int frequency = priorityQueue.poll();

            //If there is no element left after poll, It means we are done, return deletionCount.
            if (priorityQueue.size() == 0 ) {
                return deletionCount;
            }

            //Here we are comparing the polled count with the count at the head. since our PriorityQueue is in reverse order
            //Counts that are same will be grouped together. So idea is to check polled and peek and if they are same it means we
            //need to delete one occurrence of a character to make it unique, but the catch is after deletion, the count which we encountered
            //may also be the occurrence count of other character present in a queue, so we have to repeat this process.
            //number of time we delete the occurrence, we add that in our deletionCount.
            if (frequency == priorityQueue.peek()) {
                //it means we have to delete one character to make the frequency unique
                priorityQueue.add(frequency-1);

                //Number of time we delete the character to make frequency unique, we have to increase the deletionCount.
                deletionCount ++;
            }
        }
        return deletionCount;
    }
}
at No comments:

Monday, 14 September 2020

Find longest binary gap in binary representation of integer number.

Find longest length bi-valued slice in an array in java

This is a popular interview question asked in Tier-1 companies.

You are given a positive integer n, find the longest distance between two consecutive 1's in the binary representation of n.

Example:
1. Input: 9
Output: 2
9 binary representation is 1001 and there are two 0 in between 1's. so answer is 2

2. Input: 1041
Output: 5
1041 binary representation is 10000010001 and there are 5 consecutive 0's in first gap and 3 consecutive 0's in second binary gap. so answer is 5 as the highest gap among both.

3. Input: 15
Output: 0
15 binary representation is 1111 and there are no 0's in between 1's. so answer is 0

4. Input: 20
Output: 10
20 binary representation is 10100 and contains only one 0 in between 1's. so answer is 1

Algorithm

we will take 3 variables 
maxGap: for storing the result
tempGap: for storing temporary gap
oneFlag: a flag for indication that we have encountered 1 before or not.

Example: 101001, in this example when we encounter first binary gap of size 1 which would be in tempGap but later we encountered another binary gap of size 2 which is higher than before, so we need to store previous value of tempGap, that is where maxGap will be used to store whichever is highest among previous binary gaps.

Java Program to find longest binary gap in binary representation of an integer number.


package javabypatel;

public class BinaryGap {
    public static void main(String[] args) {
        System.out.println(new BinaryGap().findLongestBinaryGap(20));
    }

    public int findLongestBinaryGap(int number) {
        int maxGap = 0;
        int tempGap = 0;
        boolean oneFlag = false;

        while (number > 0) {
            int remainder = number % 2;
            number = number / 2;
            System.out.print(remainder);
            if (oneFlag) {
                if (remainder == 1) {
                    maxGap = Math.max(tempGap, maxGap);
                    tempGap = 0;
                } else {
                    tempGap ++;
                }
            } else if (remainder == 1) {
                oneFlag = true;
            }
        }
        System.out.println();
        return maxGap;
    }
}
at No comments:

Find longest length bi-valued slice in an array

Find longest length bi-valued slice in an array in java

This is a popular interview question asked in Tier-1 companies.

You are given a sequence of n integers and the task is to find the maximum slice of the array which contains no more than two different numbers.

Example:
1. Input: [1, 2, 1, 2, 2, 3, 3, 2, 3]
Output: 6
Max slice is [2, 2, 3, 3, 2, 3] which contains only two numbers 2 and 3 and the length is 6 

2. Input: [1, 2, 3]
Output: 2
Max slice is either [1, 2] or [2, 3] which contains only two numbers and the length is 2

3. Input: [1, 4, 4, 1, 4]
Output: 5 
Max slice is whole array which contains only two numbers 1 and 4 and the length is 5

4. Input: [2]
Output: 1 
Max slice is whole array which contains only one number 2 and the length is 1

Algorithm

As we are looking for bi-value slice, we will keep two pointer lastSeen and secondLastSeen which keep track of the numbers we last read.

So if the current number we are reading is one of the number we read before that is it is same as either lastSeen or secondLastSeen, then we can increase our longest bi-value slice counter(say tempCounter) by 1

So we have three variables till now, lastSeen, secondLastSeen and tempCounter to store the current longest bi-value slice.


Consider the array [1, 2, 1, 2, 2, 3, 3, 2, 3]

say we read 1, 2, 1, 2, 2 and we were good at that point, now we read element 3, so in that case new series has started but including the current number 3 we can include the previous two 2's in this series that is starting from index 3.

So instead of going back and see the last repeated number, we will keep track of this in the separate variable lastSeenNumberRepeatedCount which holds the number of times last seen value repeated in this case lastSeenNumberRepeatedCount would be 2, because when we encountered 3 at index 5, the number before 3 is 2 which first occur at index 3 and then the same number repeated that is lastSeen number repeated at index 4 so making lastSeenNumberRepeatedCount to 2.

So when we encounter 3 at index 5, we directly add the lastSeenNumberRepeatedCount to our tempCounter so it would be lastSeenNumberRepeatedCount + 1 (added 1 because starting from 3 new series has started, so including the current number 3)

So we have four variables till now, lastSeen, secondLastSeen, tempCounter and lastSeenNumberRepeatedCount.

We also need one more variable for storing our longest bi-valued slice as tempCounter will change when new series starts so what about the previous value of tempCounter which was our last longest bi-value slice till that point.

So we have five variables till now, lastSeen, secondLastSeen, tempCounter, lastSeenNumberRepeatedCount and lbs for storing result.

Java Program to find largest bi-valued slice in an array

package javabypatel;

public class LongestBiValueSlice {
    public static void main(String[] args) {
        System.out.println(new LongestBiValueSlice().getLongestSlice(new int[]{2}));
    }

    public int getLongestSlice(int[] arr) {
        int lastSeen = -1;
        int secondLastSeen = -1;
        int lbs = 0;
        int tempCount = 0;
        int lastSeenNumberRepeatedCount = 0;

        for (int current : arr) {
            if (current == lastSeen || current == secondLastSeen) {
                tempCount ++;
            } else {
                // if the current number is not in our read list it means new series has started, tempCounter value in this case will be
                // how many times lastSeen number repeated before this new number encountered + 1 for current number.
                tempCount = lastSeenNumberRepeatedCount + 1;
            }

            if (current == lastSeen) {
                lastSeenNumberRepeatedCount++;
            } else {
                lastSeenNumberRepeatedCount = 1;

                secondLastSeen = lastSeen;
                lastSeen = current;
            }

            lbs = Math.max(tempCount, lbs);
        }
        return lbs;
    }
}
at No comments:

Tuesday, 1 September 2020

Custom BlockingQueue implementation in java

Producer Consumer using custom BlockingQueue implementation in java

Implement a custom Blocking Queue is very popular interview question.

What is Blocking Queue?

BlockingQueue is a queue data structure that blocks all the threads trying to read(Consumer) the data from the queue if the queue is empty and similarly it blocks all the threads trying to add(Producer) the data to the queue if the queue is full. due to this blocking feature, the queue is known as BlockingQueue. 

Threads that are blocked for adding the data to the queue due to queue full gets unblocked when some other thread removes the data from the queue and there is a space to add new data.

Threads that are blocked for reading the data from the queue due to queue empty gets unblocked when some other thread adds the data to the queue and there is some data to read.

Note: BlockingQueue doesn't accept null values, If we try to add null, then it throws NullPointerException.
Custom BlockingQueue implementation in java
Custom BlockingQueue implementation in java

I would recommend going through below articles for better understanding of Threads and synchronization in Java.


Implement Custom BlockingQueue in Java

 
package javabypatel;

import java.util.concurrent.locks.Condition;
import java.util.concurrent.locks.Lock;
import java.util.concurrent.locks.ReentrantLock;

public class CustomBlockingQueueUsingLock {
    private Lock lock = new ReentrantLock();
    private Condition putCondition = lock.newCondition();
    private Condition takeCondition = lock.newCondition();

    private Object[] queue;
    private int queueSize;

    private int putIndex;
    private int takeIndex;
    private int count;

    public CustomBlockingQueueUsingLock(int queueSize) {
        this.queueSize = queueSize;
        queue = new Object[queueSize];
    }

    public void put(Object data) {
        lock.lock();
        try{
            while (count >= queueSize) {
                try {
                    putCondition.await();
                } catch (InterruptedException e) {
                    e.printStackTrace();
                }
            }
            System.out.println("Queuing value :" + data);
            queue[putIndex] = data;
            count++;

            if (++putIndex >= queueSize) {
                putIndex = 0;
            }
            takeCondition.signalAll();
        }  finally {
            lock.unlock();
        }
    }

    public Object take() {
        lock.lock();
        try {
            while (count == 0) {
                try {
                    takeCondition.await();
                } catch (InterruptedException e) {
                    e.printStackTrace();
                }
            }
            Object data = queue[takeIndex];
            count--;

            if (++takeIndex >= queueSize) {
                takeIndex = 0;
            }
            putCondition.signalAll();
            return data;
        } finally {
            lock.unlock();
        }
    }

    public static void main(String[] args) {
        CustomBlockingQueueUsingLock customBlockingQueue = new CustomBlockingQueueUsingLock(5);

        new Thread(() -> {
            int i = 0;
            while (i < 10) {
                System.out.println("data :" + customBlockingQueue.take());
                i++;
            }
        }, "Consumer Thread").start();

        new Thread(() -> {
            int i = 0;
            while (i < 10) {
                customBlockingQueue.put(i);
                i++;
            }
        }, "Producer Thread").start();
    }
}
 

Implement Custom Generic blocking queue using Linked list data structure and Locks in Java

package javabypatel;

import java.util.LinkedList;
import java.util.Queue;
import java.util.concurrent.locks.Condition;
import java.util.concurrent.locks.Lock;
import java.util.concurrent.locks.ReentrantLock;

public class GenericCustomBlockingQueueUsingLock<T> {
    private Queue<T> queue = new LinkedList<T>();

    private Lock lock = new ReentrantLock();
    private Condition putCondition = lock.newCondition();
    private Condition takeCondition = lock.newCondition();

    private int size;

    public GenericCustomBlockingQueueUsingLock(int size) {
        this.size = size;
    }

    public T take() throws InterruptedException {
        lock.lock();
        try {
            while (queue.isEmpty()) {
                takeCondition.await();
            }
            T data = queue.poll();

            //If say the queue is full before we take, then chances are threads trying to put would be waiting, so after taking the
            //element we will inform put threads that there is space now for you to put.
            putCondition.signal();
            return data;
        } finally {
            lock.unlock();
        }
    }

    public void put(T obj) throws InterruptedException {
        lock.lock();
        try {
            while (queue.size() == size) {
                putCondition.await();
            }
            System.out.println("Putting data :" + obj);
            queue.add(obj);

            //If say the queue is empty before we add the element to the queue, then chances are threads trying to take the element would be waiting,
            //so after adding the element we will inform take threads that there is element now for you to take.
            takeCondition.signal();
        } finally {
            lock.unlock();
        }
    }

    public static void main(String[] args) {
        GenericCustomBlockingQueueUsingLock<Integer> queue = new GenericCustomBlockingQueueUsingLock<>(10);
        new Thread(() -> {
            int i = 0;
            while (i < 20) {
                try {
                    System.out.println(queue.take());
                } catch (InterruptedException e) {
                    e.printStackTrace();
                }
                i++;
            }
        }).start();

        new Thread(() -> {
            int i = 0;
            while (i < 20) {
                try {
                    queue.put(i);
                } catch (InterruptedException e) {
                    e.printStackTrace();
                }
                i++;
            }
        }).start();
    }
}
at No comments: