Binary Search Tree Operations ( Add a node in Binary Search Tree, Search a node in Binary Search Tree ).

How to Add a Node and Search a Node in Binary Search Tree?

---

Let's see how to insert a node in binary search tree (BST) and search a node in binary search tree.

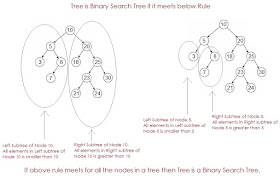
What is Binary Search Tree?
In computer science, Binary Search Trees (BST), sometimes called Ordered or sorted binary trees, are a particular type of containers: data structures that store "items" (such as numbers, names and etc.) in memory. They allow fast lookup, addition and removal of items, and can be used to implement either dynamic sets of items, or lookup tables that allow finding an item by its key (e.g., finding the phone number of a person by name).
More: https://en.wikipedia.org/wiki/Binary_search_tree

While adding a Node in a Binary Search Tree, it should follow below rules,

1. All values descending on the Left side of a node should be less than (or equal to) the node itself. 
2. All values descending on the Right side of a node should be greater than (or equal to) the node itself.

If Tree follows above protocol for all the Nodes of a tree, then Tree is called a Binary Search Tree. See below image to get better understanding of Binary Search Tree rules.

Insert node in binary search tree in Java

Search a Node in Binary Search Tree 

---

To search a data in Binary Search Tree, First compare it with root node data,

1. If the data to search is present at root node data, then return root node as we found it.
2. If key to search is greater than root’s node data, then further we will look at right subtree of root node and ignore Left subtree.
3. If key to search is smaller than root’s node data, then further we will look at left subtree of root node and ignore right subtree.

Algorithm for searching a node in binary search tree

Java Program to Insert and Search a Node in Binary Search Tree

---

Container: Node class

package javabypatel.tree;

public class Node{
 
 private Node left;
 private Node right;
 private int data;
 
 public Node(int data){
  this.data=data;
 }

 public Node getLeft() {
  return left;
 }

 public void setLeft(Node left) {
  this.left = left;
 }

 public Node getRight() {
  return right;
 }

 public void setRight(Node right) {
  this.right = right;
 }

 public int getData() {
  return data;
 }

 public void setData(int data) {
  this.data = data;
 }
}

Return type of addNode method returns Node

---

package javabypatel.tree;

public class AddNodeInBinarySearchTree {

 public static void main(String[] args) {
  new AddNodeInBinarySearchTree();
 }
 
 public AddNodeInBinarySearchTree(){
  Node rootNode=null; 
  rootNode  = addNode(rootNode, 50);
  rootNode  = addNode(rootNode, 20);
  rootNode  = addNode(rootNode, 60);
  rootNode  = addNode(rootNode, 10);
  rootNode  = addNode(rootNode, 25);

  printTreeInOrder(rootNode);
  
  System.out.println("Result :"+searchNode(rootNode, 60));
 }
 
 private Node addNode(Node rootNode, int data) {
  if(rootNode==null){
   return new Node(data);
  }else{
   if(data > rootNode.getData()){
    rootNode.setRight(addNode(rootNode.getRight(), data));
   }else{
    rootNode.setLeft(addNode(rootNode.getLeft(), data));
   }
  }
  return rootNode;
 }

 private boolean searchNode(Node rootNode, int data){
  if(rootNode==null){
   return false;
  }
 
  if(rootNode.getData()==data){
   return true;
  }
 
  if(data < rootNode.getData()){
   return searchNode(rootNode.getLeft(), data);
  }else{
   return searchNode(rootNode.getRight(), data);
  }
 }
 
 private void printTreeInOrder(Node rootNode){
  if(rootNode==null)
   return;
  printTreeInOrder(rootNode.getLeft());
  System.out.print(rootNode.getData() + " ");
  printTreeInOrder(rootNode.getRight());
 }

}

Return type of addNode method returns void

---

package javabypatel.tree;

public class AddNodeInBinarySearchTree {

 private Node rootNode;

 public static void main(String[] args) {
  new AddNodeInBinarySearchTree();
 }
 
 public AddNodeInBinarySearchTree(){
  addNode(rootNode, 20); 
  addNode(rootNode, 10); 
  addNode(rootNode, 30); 
  addNode(rootNode, 5); 
  addNode(rootNode, 15);
  
  printTreeInOrder(rootNode);
  
  System.out.println("Result :"+searchNode(rootNode, 30));
 }
 
 private void addNode(Node startNode, int data){
  if(startNode==null){
   this.rootNode = new Node(data);
  }else{
   if(data > startNode.getData()){
    if(startNode.getRight()!=null)
     addNode(startNode.getRight(), data);
    else
     startNode.setRight(new Node(data));
   }else{
    if(startNode.getRight()!=null)
     addNode(startNode.getLeft(), data);
    else
     startNode.setLeft(new Node(data));
   }
  }
 }
 
 private boolean searchNode(Node rootNode, int data){
  if(rootNode==null){
   return false;
  }
 
  if(rootNode.getData()==data){
   return true;
  }
 
  if(data < rootNode.getData()){
   return searchNode(rootNode.getLeft(), data);
  }else{
   return searchNode(rootNode.getRight(), data);
  }
 }

 private void printTreeInOrder(Node rootNode){
  if(rootNode==null)
   return;
  printTreeInOrder(rootNode.getLeft());
  System.out.print(rootNode.getData() + " ");
  printTreeInOrder(rootNode.getRight());
 }
}

---

Find Kth LARGEST element in BST(Binary Search Tree)

Check whether Binary Tree is foldable or not.

Check if two nodes are cousins in a Binary Tree.

Get Level/Height of node in binary tree

Print nodes at K distance from Leaf node in Binary tree.

Construct a Binary Tree from In-order and Post-order traversals.

Print Nodes in Top View of Binary Tree.

Zig Zag Traversal of Binary Tree.

Enjoy !!!! 

If you find any issue in post or face any error while implementing, Please comment.