Convert Sorted Linked list to balanced Binary Search Tree
Convert sorted list to binary search tree
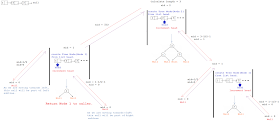
Lets simplify the question statement, Given a singly Linked List where elements are sorted in ascending order convert it to a height balanced BST.
A Binary Search Tree is called balanced if the height of left subtree and height of right subtree of Root differ by at most 1.
Lets understand the problem statement graphically and it will be more clear,
Solution to convert sorted list to BST is very similar to Convert Sorted Array to BST
Approach 1:
To convert linked list to balanced BST,
Complexity of above approach is O(n log n) because every time we need to find middle node.
Let see some better approach with time complexity O(n).
In above approach, we created a Tree from Top to Bottom that is created a Root Node first (that is why it require to calculate middle element) then created a Left Subtree and Right Subtree.
Approach 2:
In this approach we will start creating Tree from Bottom to Up.
Root Node of Tree will be created at last.
Main idea of this approach is to get the linked list size and keep breaking the length into equal parts until it reaches 0.
Once it reaches 0, return, upon return pick one by one element of linked list and make it tree node.
Note: we are reading Left child first, then root and then right child.
Convert sorted list to binary search tree
Lets simplify the question statement, Given a singly Linked List where elements are sorted in ascending order convert it to a height balanced BST.
A Binary Search Tree is called balanced if the height of left subtree and height of right subtree of Root differ by at most 1.
Lets understand the problem statement graphically and it will be more clear,
Algorithm
Solution to convert sorted list to BST is very similar to Convert Sorted Array to BST
Approach 1:
To convert linked list to balanced BST,
- Get the middle node of the linked list and make it Root Node.
Now the list is splitted into 2 parts left side of middle node and right side of middle node. - Recursively do same for left side and right side.
a) find the middle element of left side and make it Left child of Root Node created in step 1.
b) find the middle element of right side and make it Right child of Root Node created in step 1.
Complexity of above approach is O(n log n) because every time we need to find middle node.
Let see some better approach with time complexity O(n).
In above approach, we created a Tree from Top to Bottom that is created a Root Node first (that is why it require to calculate middle element) then created a Left Subtree and Right Subtree.
Approach 2:
In this approach we will start creating Tree from Bottom to Up.
Root Node of Tree will be created at last.
- Logic is to first calculate the size of List and once size of Linked List is identified,
- Repeat the same step as we did in first approach, but instead of identifying the middle node, we will divide the list (length of list/2) into 2 parts recursively into left side and right side. (Postpone creation of node at last, so that leaf nodes that is bottom nodes are created first and then top nodes)
- By breaking the list into 2 parts recursively, at one point we will left by only one node and that will be leaf node, create a Tree node by that element and return a node to previous recursive call.
Main idea of this approach is to get the linked list size and keep breaking the length into equal parts until it reaches 0.
Once it reaches 0, return, upon return pick one by one element of linked list and make it tree node.
Note: we are reading Left child first, then root and then right child.
Sorted Linked list to BST Java Program
package javabypatel;
public class SortedLinkedListToBalancedBST {
LinkedListNode head;
public static void main(String[] args) {
new SortedLinkedListToBalancedBST();
}
public SortedLinkedListToBalancedBST(){
head = new LinkedListNode(1);
LinkedListNode lln2 = new LinkedListNode(2);
LinkedListNode lln3 = new LinkedListNode(3);
LinkedListNode lln4 = new LinkedListNode(4);
LinkedListNode lln5 = new LinkedListNode(5);
LinkedListNode lln6 = new LinkedListNode(6);
LinkedListNode lln7 = new LinkedListNode(7);
head.setNext(lln2);
lln2.setNext(lln3);
lln3.setNext(lln4);
lln4.setNext(lln5);
lln5.setNext(lln6);
lln6.setNext(lln7);
Node balancedBSTTopDown = sortedLinkedListToBalancedBSTTopDown(head);
printTreeInOrder(balancedBSTTopDown);
Node balancedBSTBottomUp = sortedLinkedListToBalancedBSTBottomUp(head);
printTreeInOrder(balancedBSTBottomUp);
}
private Node sortedLinkedListToBalancedBSTBottomUp(LinkedListNode list){
int length = getLengthOfLinkedList(list);
return sortedLinkedListToBST(length);
}
private Node sortedLinkedListToBST(int length){
if(length <= 0){
return null;
}
Node left = sortedLinkedListToBST(length/2);
Node root = new Node(head.getData());
root.setLeft(left);
head = head.getNext();
root.setRight(sortedLinkedListToBST(length - length/2 - 1));
return root;
}
private int getLengthOfLinkedList(LinkedListNode list){
if(list==null){
return 0;
}
int count = 1;
while((list = list.getNext()) != null){
count++;
}
return count;
}
private Node sortedLinkedListToBalancedBSTTopDown(LinkedListNode lln){
if(lln==null){
return null;
}
if(lln.getNext()==null){
return new Node(lln.getData());
}
LinkedListNode tortoise = lln;
LinkedListNode hare = lln;
LinkedListNode previous = null;
while(hare!=null && hare.getNext()!=null){
hare = hare.getNext().getNext();
previous = tortoise;
tortoise = tortoise.getNext();
}
LinkedListNode middle = tortoise;
if(previous!=null){
middle = previous.getNext();
previous.setNext(null);
}
Node node = new Node(middle.getData());
node.setLeft(sortedLinkedListToBalancedBSTTopDown(lln));
node.setRight(sortedLinkedListToBalancedBSTTopDown(middle.getNext()));
return node;
}
private void printTreeInOrder(Node rootNode){
if(rootNode==null)
return;
printTreeInOrder(rootNode.getLeft());
System.out.print(rootNode.getData() + " ");
printTreeInOrder(rootNode.getRight());
}
}
package javabypatel;
public class Node{
private Node left;
private Node right;
private int data;
public Node(int data){
this.data=data;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
}
package javabypatel;
public class LinkedListNode{
private int data;
private LinkedListNode next;
public LinkedListNode(int data) {
this.data = data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public LinkedListNode getNext() {
return next;
}
public void setNext(LinkedListNode next) {
this.next = next;
}
}
You may also like to see
Convert Sorted Array to Balanced Binary Search Tree
Exception Handling Interview Question-Answer
Method Overloading - Method Hiding Interview Question-Answer
Advanced Multithreading Interview Questions-Answers In Java
Type Casting Interview Questions-Answers In Java
How Thread.join() in Java works internally
How is ambiguous overloaded method call resolved in java
Enjoy !!!!
If you find any issue in post or face any error while implementing, Please comment.



No comments:
Post a Comment