Construct a Binary Tree from In-order and Pre-order traversals.

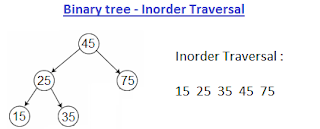
How to construct a Binary Tree from given In order and Pre order traversals.

---

Let us first understand what we want to achieve? what is the input and what will be the expected output?

Question:
Two traversals are given as input,

  int inorder[] =  {20, 30, 35, 40, 45, 50, 55, 60, 70};
  int preorder[] = {50, 40, 30, 20, 35, 45, 60, 55, 70};

By using above 2 given In order and Pre Order traversal, construct Binary Tree like shown below,

First let us understand what does In order and Pre order traversal mean?

---

In-order traversal is traversing a Tree in which Left Node is read first, then root node and then right node and hence the In-order traversal of above tree is,
In-order traversal : 20  30  35  40  45  50  55  60  70

Pre-order traversal is traversing a Tree in which root node is read first and then Left Node is read and then right node and hence the Pre-order traversal of above tree is,
Pre-order traversal : 50  40  30  20  35  45  60  55  70

From the above example, we can see that 
Root element will be present at first position in Pre-order traversal 
(50  40  30  20  35  45  60  55  70)
(since Root nodes of a Tree are read first, then Left nodes and then Right Node.)

So root node will be present at first, but by simply looking at given Pre order traversal it is not possible to identify which element is left child/sub-tree of root node and right child/sub-tree of root node as we are not aware of exact position where the left nodes started and ended in Pre-order traversal. 

For finding the Left and Right child's we will use In-order traversal.
So with the help of alone Post-order or Pre-order, it is not possible to build a Tree, we require In-order for finding Left and Right child'/sub-tree.

More details on In Order and Level Order traversal: In Order and Pre Order Traversal.

Algorithm

---

We just saw that first element of Pre order traversal is root node.

Step 1:
Read the first element from Pre order traversal which is root node.
Now, we come to know which is root node.(in our case it is 50) Step 2:
Search the same element (element 50) in In-order traversal, 
when the element is found in In-order traversal, then we can very well say that all the elements present before the node found are Left children/sub-tree and all the elements present after the node found are Right children/sub-tree of node found. (as in In-order traversal Left child's are read first and then root node and then right nodes.)

In our example,  
(20, 30, 35, 40, 45)  will be part of Left Sub-tree of Node 50.
(55, 60, 70) will be part of Right Sub-tree of Node 50.

Now we got the fresh inOrder array (20, 30, 35, 40, 45) and (55, 60, 70)
Repeat the  Step 1 and Step 2 for new inOrder arrays.

So, keeping the above rule in mind, 
We will find the root node from Pre-order traversal and then left child's and right child's from In-order traversals like shown below, 

So if we repeat the process, we will get our Binary Tree ready.

How we will decide the number of elements from inorder array and preorder array will be the part of Left sub-tree and Right sub-tree in each iteration.

---

From the above image, we can see that Node 50 in In-order array divides the Tree in 2 parts,
Left sub-tree and Right sub-tree.

So, first we saw that first element in preorder array is a rootNode, 

checking the same node in inorder array will give you 2 trees.

Lets call position of element 50 found in inorder array as INDEX

Let us understand what this 2 lines mean in below program

 node.setLeft(constructTreeFromInOrderAndPreOrder(inorder, inStart, index-1, preorder, preStart+1, preStart+(index-inStart)));
 node.setRight(constructTreeFromInOrderAndPreOrder(inorder, index+1, inEnd, preorder, preStart+(index-inStart)+1, preEnd));

Left Subtree

---

1. inOrder array

----------------------------------------------------------------------------------------------

    1. left sub tree start index = inStart

    2. left sub tree end index  = 

        all the elements present before element found.

        (element found is Node 50 in our  example)
        So in general we can say, index of element found in inOrder array (INDEX) - 1

2. preOrder array

---------------------------------------------------------------------------------------------- 

    1. left sub tree start index = preStart + 1

          Example : preStart + 1 because, Node 50 is already covered and new Left sub tree start will be
          excluding Node 50.

    2. right sub tree end index =  preStart + INDEX

             preStart + INDEX = this will give us the last index of the element that need to

             be considered. (endIndex)
        
Right Subtree

---

 1. inOrder array

 ----------------------------------------------------------------------------------------------

    1. Right sub tree start index = index of element found in inOrder array (INDEX) + 1
    2. right sub tree end index = inEnd

2. preOrder array

 ----------------------------------------------------------------------------------------------

    1. left sub tree start index =

           1. calculating startIndex of right sub-tree is simple,
               It will be endIndex of left sub-tree + 1.
               = left sub tree end index     + 1.
               = (preStart + INDEX)       + 1

 
    2. right sub tree end index = preEnd.

Java Program to construct a Binary Tree from given Inorder and Pre order traversals.

---

ConstructBinaryTreeFromInorderAndPreOrderTraversal.java

package javabypatel.tree;

public class ConstructBinaryTreeFromInorderAndPreOrderTraversal {
 
 public static void main(String[] args) {
  new ConstructBinaryTreeFromInorderAndPreOrderTraversal();
 }

 public ConstructBinaryTreeFromInorderAndPreOrderTraversal() {
  int inorder[] =  {20, 30, 35, 40, 45, 50, 55, 60, 70};
  int preorder[] = {50, 40, 30, 20, 35, 45, 60, 55, 70};

  Node n = constructTree(inorder, preorder);
  System.out.println(n);
 }

 private static Node constructTree(int[] inorder, int[] preorder) {
  return constructTreeFromInOrderAndPreOrder(inorder, 0, inorder.length-1, preorder, 0, preorder.length-1);
 }
 
 private static Node constructTreeFromInOrderAndPreOrder(int[] inorder, int inStart, int inEnd, int[] preorder, int preStart, int preEnd) {
  if(inStart>inEnd){
   return null;
  }

  if(inStart==inEnd){
   return new Node(inorder[inStart]);
  }
  
  Node node = new Node(preorder[preStart]);

  int index=0;
  for (int i = 0; i < inorder.length; i++) {
   if(preorder[preStart]==inorder[i]){
    index = i;
    break;
   }  
  }

  node.setLeft(constructTreeFromInOrderAndPreOrder(inorder, inStart, index-1, preorder, preStart+1, preStart+(index-inStart)));
  node.setRight(constructTreeFromInOrderAndPreOrder(inorder, index+1, inEnd, preorder, preStart+(index-inStart)+1, preEnd));

  return node;
 }
}

Node.java

package javabypatel.tree;

public class Node {
 private int data;
 private Node left;
 private Node right;
 private Node nextRight;

 public Node(int data) {
  this.data=data;
 }

 public int getData() {
  return data;
 }
 public void setData(int data) {
  this.data = data;
 }
 public Node getLeft() {
  return left;
 }
 public void setLeft(Node left) {
  this.left = left;
 }
 public Node getRight() {
  return right;
 }
 public void setRight(Node right) {
  this.right = right;
 }
 public Node getNextRight() {
  return nextRight;
 }
 public void setNextRight(Node nextRight) {
  this.nextRight = nextRight;
 }
}

You may also like to see

---

Construct a Binary Tree from In-order and Post-order traversals.

Construct a Binary Tree from In-order and Level-order traversals.  

Top Binary tree interview questions in Java

Find Kth SMALLEST element in BST(Binary Search Tree)

Check whether Binary Tree is foldable or not.

Check if two nodes are cousins in a Binary Tree.

Get Level/Height of node in binary tree

Print nodes at K distance from Leaf node in Binary tree.

Construct a Binary Tree from In-order and Post-order traversals.

Print Nodes in Top View of Binary Tree.

Zig Zag Traversal of Binary Tree.

Enjoy !!!! 

If you find any issue in post or face any error while implementing, Please comment.