Top 10 Matrix Interview Questions in Java

Top 10 Matrix Interview Questions

---

We will look at Most commonly asked Top 10 Matrix interview questions on Java.
Matrix interview questions are frequently asked in Amazon, Microsoft and many other companies.

Frequently asked Top 10 Matrix Interview Questions.

---

Question 1: Rotate matrix by 90 degree. (Given N*M Matrix, Rotate it by 90 degrees.)
Answer:
There are 2 ways to Rotate a Matrix by 90 degrees

1. Using extra Memory. 
2. In Place.

In this post, we will focus on Rotating a Matrix by 90 degrees clockwise using Extra memory. 

For Rotating a matrix to 90 degrees clockwise, We need to transform each row of a Matrix to a column in rotated matrix. (Check the rotated matrix image above)

It is very easy to solve this problem if it is well understood. 

What will be Rows and Columns of Rotated Result Matrix?
For rotating matrix to 90 degrees, we need to transform rows into columns and columns to rows in a result matrix. So number of rows in rotated matrix will be equal to number of columns of original matrix and number of columns in rotated matrix will be equal to number of rows.

int[][] rotatedMatrix = new int[colsOfOriginalMatrix][rowsOfOriginalMatrix]

 More...

---

Question 2: Rotate Matrix by 90 degrees clockwise Inplace. (Given N*M Matrix, Rotate it by 90 degrees Inplace.)
Answer:
There are 2 ways to Rotate a Matrix by 90 degrees

1. In Place.
2. Using extra Memory.

For Rotating a matrix to 90 degrees in-place, it should be a square matrix that is same number of Rows and Columns otherwise inplace solution is not possible and requires changes to row/column.
 

For rotating a matrix to 90 degrees, we will start rotating it Layer by Layer.
Rotate first outer layer by 90 degrees, Rotate 2nd inner layer by 90 degree, Rotate 3rd inner layer by 90 degree and so on,

We will further break the problem of Rotating each layer to rotate each cell of layer by 90 degrees More...

---

Question 3: Print Matrix in Spiral form. (Given a Matrix(2D array), print it in spiral form.)
Answer:
There are 2 ways to print matrix in Spiral order. 

1. Iterative. 
2. Recursive.

In this approach, we will focus on Iterative approach.

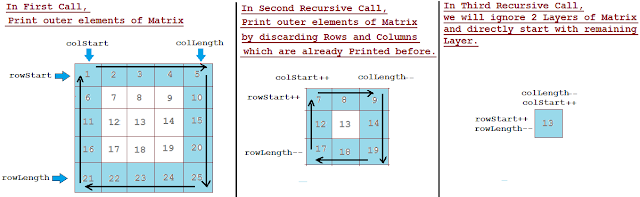
In Iterative approach, we need to maintain 4 variables rowStart, rowLength, colStart, colLength which help in printing matrix in Spiral way.

STEP 1: Left to Right.
Move variable i from rowStart till colLength. (Print data from first row till last column.)

STEP 2: Top to Bottom. More...

---

Question 4: Print Matrix in Spiral order using Recursion. (Given a Matrix(2D array), print it in spiral form Recursively.)
Answer:
There are 2 ways to print matrix in Spiral order. 

1. Iterative. 
2. Recursive.

In this approach, we will focus on Recursive approach.

In Iterative approach, we need to maintain 4 variables rowStart, rowLength, colStart, colLength which help in printing matrix in Spiral way.

In Recursive approach, we will be requiring same 4 variable and follow the same process, only difference in this approach will be, after printing first outer Layer of Matrix elements, before moving into inner layers of Matrix, we will check whether next inner layer of Matrix is present or this is end of all Layers.

If Matrix has inner Layer present, we will increment rowStart++, colStart++ and decrement rowLength--, colLength--, which now points to inner matrix layer and pass this variable to next recursive call. More...

---

Question 5: Transpose of Matrix in Java. (You are given a M * N matrix, find Transpose of Matrix.)
Answer:
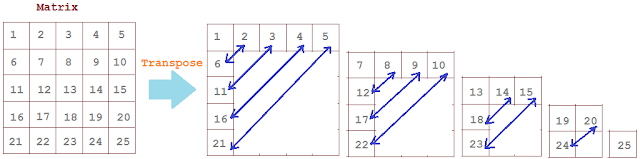
Transpose of matrix is obtained by interchanging rows and columns of a matrix that is by changing rows to columns and columns to rows.  

Transpose of given matrix can be obtained by changing its rows to columns and columns to rows.

Create a new Matrix as Transpose Matrix of size,

1. Rows     = Total column of original matrix.
2. Column = Total rows of original matrix.

Iterate through Original matrix, and fill Transpose Matrix data by interchanging rows to column and column to rows as shown below,

TransposeMatrix[col][row] = OriginalMatrix[row][col]. More...

---

Question 6: Transpose of Matrix Inplace. (You are given a M * N matrix, find Transpose of Matrix in-place.)
Answer:
Transpose of matrix is obtained by interchanging rows and columns of a matrix that is by changing rows to columns and columns to rows.  

Note: For Inplace transpose, Matrix should always be Square Matrix that is having same number of Rows and Columns.

Transpose of given matrix can be obtained by changing its rows to columns and columns to rows.

1. Iterate through a Matrix and swap data of rows and columns.
2. While iterating make sure, Column start from where Row start.

Java Program to More...

---

Question 7: Find a Saddle point in Matrix.
Answer:
Given a matrix of n x n size, Find saddle point of matrix.

What is Saddle point of Matrix?
Element is said to be Saddle point of Matrix if it is both a minimum of its row and a maximum of its column or vice versa.

A matrix may have 1 or 2 saddle points or may not have a saddle point. Lets understand what will be input and expected output with the help of an example.
For finding Saddle Point,

1. Traverse the Matrix row by row and for each row, find the minimum element in that row. let say you find the minimum element at index j. 
2. Check the maximum element on same column j. More...

---

Question 8: Search in a row wise and column wise sorted matrix.
Answer:
Given an n x n matrix, where every row and column is sorted in increasing order.  Given a number k, how to decide whether this k is in the matrix.

There are many approach to solve this problem, Lets see few of them.

Approach 1:
Check for the number one by one by looking at each element of the array.
This approach is not efficient as in worst case we need to traverse complete matrix to identify whethet element is present or not.

Approach 2:
As matrix ix sorted, we can apply binary search on each row and identify whether element is present or not.

Approach 3: In this approach, we will start our search by looking at Right most element of first row. More...

---

Question 9: Count zeros in a row wise and column wise sorted matrix.
Answer:
Count zeros in a row wise and column wise sorted matrix

There are many approach to solve this problem, Lets see few of them.

Approach 1:
Initialise counter = 0 and check for each element of the array and increment counter if you encounter 0. This approach is not efficient as in worst case we need to traverse complete matrix to identify whether element is present or not.

Approach 2:
As matrix is sorted, we can apply binary search and identify start position of 0 in each row and sum count of 0 of each row.

Approach 3:
In this approach, we will start our search by looking at Right most element of first row More...

---

Question 10: Print Matrix Diagonally OR Diagonal order of Matrix.
Answer:
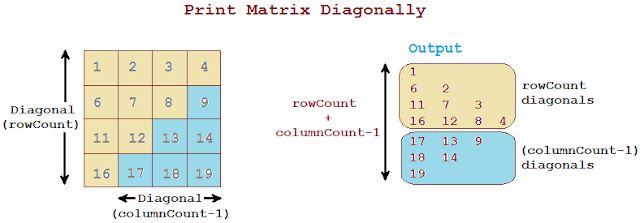
Given a Matrix / 2D array, Print all elements of Matrix in Diagonal order.

If we observe the Matrix, there are 2 set of Diagonals,

1. rowCount diagonals 
2. (colCount - 1) diagonals.

We will first print the rowCount diagonals and then print the remaining columnCount-1 diagonals. More...

You may also like to see

---

Top Binary Tree Interview Questions

When to use Interface in java with example

Interface Vs Abstract class in Java OOPS.

Top Java Interface Interview Questions and Answers

When to use interface and abstract class in Java? what is the difference between them?

Java Multithreading and Concurrency Interview Questions and Answers with Example

Advanced Multithreading Interview Questions In Java

How ConcurrentHashMap works and ConcurrentHashMap interview questions.

Enjoy !!!! 

If you find any issue in post or face any error while implementing, Please comment.