Print power set of any given set OR Print all subsets of a set OR
Find all subsets of a set OR Print all subset of an array.
Given a set of numbers, print all the possible subsets of it including empty set.
What is Power Set?
In mathematics, the power set (or powerset) of any set S, written P(S), is the set of all subsets of S, including the empty set and S itself.Let's understand it with help of example.
Case 1:
Input: Set(S) = [1,2]
Output: PowerSet P(S) = [[ ], [2], [1], [2, 1]]
Case 2:
Input: Set(S) = [a,b,c]
Output: PowerSet P(S) = [[ ], [a], [b], [c], [a,b], [a, c], [b, c], [a, b, c]]
Solution
There can be many approach to solve this problem, here we will look at 2 simple approaches.
1. Using Tree representation approach.
2. Using Bit manipulation approach.
Tree Representation Approach
In this approach, we will draw a Tree like shown below,
There are 2 possibilities for each item of a set, It will be either included in a subset or not included.
Based on this fact, Lets draw a Tree for given Set [a, b, c].
There are 2 possibilities of "a". It will be either included in a subset or not included.
Similarly, For each possibilities of "a", again there are 2 possibilities for "b".
"b" will be included for each possibilities of "a" or not included.
Similarly, For each possibilities of "b", again there are 2 possibilities for "c".
Again, For "c", there are 2 possibilities either it will be considered or will be ignored in a subset.
Stop as there are no more items in a set remaining. Our Tree is complete and will look as shown in image above.
Lets understand our example and draw a Tree for it.
Set [a, b, c].
"a" is included.
1. "b" will be included in a subset.
2. "c" will be included in a subset. END- No more element in Set.
2. "c" will not be included in a subset. END- No more element in Set.
1. "b" will not be included in a subset.
2. "c" will be included in a subset. END- No more element in Set.
2. "c" will not be included in a subset. END- No more element in Set.
"a" is not included.
1. "b" will be included in a subset.
2. "c" will be included in a subset. END- No more element in Set.
2. "c" will not be included in a subset. END- No more element in Set.
1. "b" will not be included in a subset.
2. "c" will be included in a subset. END- No more element in Set.
2. "c" will not be included in a subset. END- No more element in Set.
Now, read the Tree from Bottom to Root. Wherever there is Yes, include the item in a subset, ignore otherwise.
"a" is included.
1. "b" will be included in a subset.
2. "c" will be included in a subset. END- No more element in Set. = [ c, b, a ]
2. "c" will not be included in a subset. END- No more element in Set. = [ b, a ]
1. "b" will not be included in a subset.
2. "c" will be included in a subset. END- No more element in Set. = [ c, a ]
2. "c" will not be included in a subset. END- No more element in Set. = [ a ]
"a" is not included.
1. "b" will be included in a subset.
2. "c" will be included in a subset. END- No more element in Set. = [ c, b ]
2. "c" will not be included in a subset. END- No more element in Set. = [ b ]
1. "b" will not be included in a subset.
2. "c" will be included in a subset. END- No more element in Set. = [ c ]
2. "c" will not be included in a subset. END- No more element in Set. = [ ]
Subset or PowerSet of [a, b, c] is [ [ c, b, a ], [ b, a ], [ c, a ], [ a ], [ c, b ], [ b ], [ c ], [ ] ]
Understanding Program
Algorithm we will use for printing subset of a set is,
Step 1. Collect empty subset ([ ]) first because empty subset will be subset of any set including null set.
Step 2. Now, For each item of a Set, Iterate subsets already found and
1. Include a item in each subset and
2. Not include a item in each subset.
Java Program for printing Subsets of set using Tree representation approach.
package javabypatel;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
public class FindAllSubsetOfSet {
public static void main(String[] args) {
System.out.println("\n"+createSubsetUsingTree("A"));
}
private static List<String> createSubsetUsingTree(String str){
List<String> result = new ArrayList<String>(); // take set if you want unique results.
result.add("[]");
//If str is not null, then process further otherwise return empty set.
if(str!=null && str.length()>0){
//Iterate each element of a set
for (int i = 0; i < str.length(); i++) {
//Working on str.charAt(i);
//Store the result of subset of str.charAt(i) in tempList.
List<String> tempList = new ArrayList<String>();
//Add str.charAt(i) in each item of result.
Iterator<String> iter = result.iterator();
while(iter.hasNext()){
String val = iter.next();
// If val is [], it means str.charAt(i) is not included, So include it in result.
if(val.equals("[]")){
tempList.add("[" + str.charAt(i) + "]");
}else{
//For each item, there will be 2 subset, one including it and one without including it.
//If val is not [], it means it already contain some subset without str.charAt(i), So just include it.
tempList.add("[" + val.substring(1,val.length()-1) + ", " + str.charAt(i) + "]");
}
}
//Add all subsets present in tempList to final result.
result.addAll(tempList);
}
}
return result;
}
}
Using List instead of String (Leetcode 78. Subsets)
Recursive:
package javabypatel;
import java.util.ArrayList;
import java.util.List;
class Solution {
public List<List<Integer>> subsets(int[] nums) {
if(nums == null) {
return null;
}
List<List<Integer>> result = new ArrayList<>();
subsetsHelper(nums, 0, new ArrayList<Integer>(), result);
return result;
}
void subsetsHelper(int[] nums, int index, List<Integer> tempResult, List<List<Integer>> res) {
if (index >= nums.length) {
res.add(tempResult);
return;
}
List<Integer> tempList = new ArrayList<>(tempResult);
tempResult.add(nums[index]);
subsetsHelper(nums, index+1, tempResult, res);
subsetsHelper(nums, index+1, tempList, res);
}
}
Using List instead of String (Leetcode 78. Subsets) Iterative:package javabypatel;
import java.util.ArrayList;
import java.util.List;
class Solution {
public List<List<Integer>> subsets(int[] nums) {
if(nums == null) {
return null;
}
List<List<Integer>> result = new ArrayList<>();
result.add(new ArrayList<Integer>());
for (int i=0; i<nums.length; i++) {
List<List<Integer>> tempResult = new ArrayList<>();
for (int j=0; j<result.size(); j++) {
List<Integer> temp = result.get(j);
//Add
List<Integer> newTemp = new ArrayList<>(temp);
newTemp.add(nums[i]);
tempResult.add(newTemp);
//Keep as is
tempResult.add(temp);
}
result = tempResult;
}
return result;
}
}
Recursive Approach
package javabypatel;
static void printSubsequences(int arr[], int index, String str) {
if (index >= arr.length) {
System.out.println("[" + str + "]");
return;
}
printSubsequences1(arr, index + 1, str + arr[index]);
printSubsequences1(arr, index + 1, str);
}
Another Recursive Approach
package javabypatel;
static void printSubsequences(int arr[], int index, String str) {
if (index >= arr.length) {
System.out.println(str);
return;
}
System.out.println(str);
for (int i = index; i < arr.length; i++) {
String str2 = str + arr[i];
printSubsequences(arr, i + 1, str2);
}
}
Bit Manipulation Approach
In this approach we will use Bits Manipulation for printing Subset of a set.
Before going ahead, first lets understand how to check any bit is set in a byte.
Binary representation of a number 1 = 0001, 2 = 0010, ...., 5 = 0101, ....
How to identify whether LSB, that is bit at position 0 is set in 5(0101)?
Solution:
Do a Logical AND of 1 and 5 that is (0001 & 0101).
If the result is greater than 0, then LSB, that is bit at position 0 is set in value 5.
How to identify whether bit at position 1 is set in 5(0101)?
Solution:
Do a Logical AND of 2 and 5 that is (0010 & 0101).
If the result is greater than 0, then bit at position 1 is set
So, to generalize it, if we want to check nth bit is set in a number,
Step 1. We will first take binary representation of 1 (0001),
Step 2. Move the LSB in binary representation of 1 to nth position.
Eg: If we want to check whether bit at position 2 is set, then move 1 two times on right side,
= 1 << 2
= 0001 << 2
= 0100
Step 3. Once the LSB of binary 1 is moved to nth position, which we want to check,
just do logical AND of binary representation of 1 with the number,
If the result is greater than 0, then the bit is set, not otherwise.
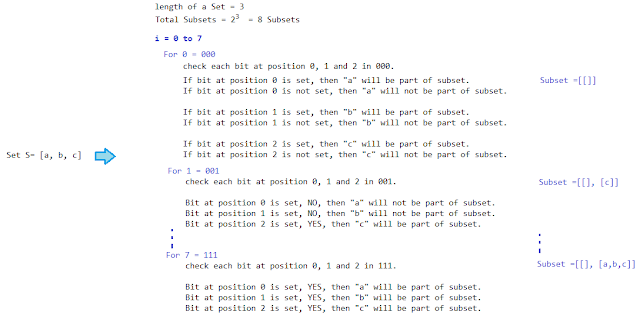
If we want to find subset of 3 characters [a, b, c], then how many total subset can be made out of it?
If you observe, the number of subsets equals to 2 to the power of the number of elements in the set.
Number of subsets that can be made from set of 3 characters [a, b, c] is 2^3 = 8 subsets.
Number of subsets that can be made from set of 4 characters [a, b, c, d] is 2^4 = 16 subsets.
So, If there are n characters [a, b, c.... n] in a set, then there will be 2^n total subsets.
How to find total number of subsets possible using bit manipulation?
By shifting the bit representation of the number 1 by n, we will get 2^n.
Thus, if we shift the bit string of 1 by the number of elements in the given set, we'll get the number of subsets for that set.
For example, if we have S = [a, b, c], length of set here is 3,
So, for finding total subsets, we have to shift binary 1, 3 times,
1 << 3 = (0001 << 3) = (1000) = 2^3 = 8 subsets of set S.
If we compare subset of [a, b, c] to binaries representation of numbers from 0 to 7, we can find a relation with the bit sets in each number to subsets of [a, b, c].
Understanding Program
Java Program for printing Subsets of set using Bit Manipulation approach.
package javabypatel;
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class FindAllSubsetOfSet {
public static void main(String[] args) {
List<Object> list = new ArrayList<Object>();
list.add("a");
list.add("b");
list.add("c");
System.out.println(getSubsetUsingBitMap(list));
}
private static Set<Set<Object>> getSubsetUsingBitMap(List<Object> list){
Set<Set<Object>> result = new HashSet<Set<Object>>();
int numOfSubsets = 1 << list.size(); //OR Math.pow(2, list.size())
// For i from 0 to 7 in case of [a, b, c],
// we will pick 0(0,0,0) and check each bits to see any bit is set,
// If set then element at corresponding position in a given Set need to be included in a subset.
for(int i = 0; i < numOfSubsets; i++){
Set<Object> subset = new HashSet<Object>();
int mask = 1; // we will use this mask to check any bit is set in binary representation of value i.
for(int k = 0; k < list.size(); k++){
if((mask & i) != 0){ // If result is !=0 (or >0) then bit is set.
subset.add(list.get(k)); // include the corresponding element from a given set in a subset.
}
// check next bit in i.
mask = mask << 1;
}
// add all subsets in final result.
result.add(subset);
}
return result;
}
}
You may also like to see
Write a program to print all permutations of a given string without repetition. (Repetition of characters is not allowed).
Write a program to print all permutations of a given string with repetition. (Repetition of characters is allowed).
Print all combinations/permutations of a string of length k that can be formed from a set of n characters
How ConcurrentHashMap works and ConcurrentHashMap interview questions
How Much Water Can A Bar Graph with different heights can Hold
Interview Questions-Answer Bank
Enjoy !!!!
If you find any issue in post or face any error while implementing, Please comment.














Post a Comment