What is Binary Tree Traversal?
Binary tree traversal is a way to read a tree by visiting each node in a particular manner.
We will look into three popular binary tree traversal, Inorder, Preorder and Postorder along with example.
Note: Tree traversal (Inorder, Preorder and Postorder) are classified as a part of Graph traversal because Tree is a special kind of Graph.
There are mainly 2 types of Graph traversal algorithms Breadth first traversal and Depth First traversal and is divided as follows,
- Depth First Traversal
- Inorder traversal
- Preorder traversal
- Postorder traversal
- Breadth First Traversal
- Level Order Traversal
Depth First Traversal
Depth First Traversal is a traversing way where all the children of Left node are read first and then all the children of right node, that is once we start visiting a Left node, we cannot visit right node until and unless all child of left node are not visited.
This way of reading a binary tree leads to 3 ways of Traversal,
- Inorder traversal
- Preorder traversal
- Postorder traversal
- Traverse the left subtree,
- Visit the root node and print data of that node, and
- Traverse the right subtree.
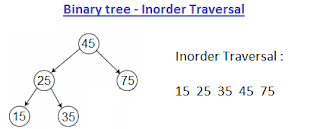 |
| Inorder traversal of binary tree example |
Detailed explanation on Inorder traversal: Inorder traversal of binary tree
Preorder traversal: To traverse a binary tree in Preorder, following operations are carried-out
- Visit the root node and print data of that node.
- Traverse the left subtree, and
- Traverse the right subtree.
 |
| Preorder traversal of binary tree example |
Detailed explanation on Preorder traversal: Preorder traversal of binary tree
Postorder traversal: To traverse a binary tree in Postorder, following operations are carried-out
- Traverse the left subtree,
- Traverse the right subtree, and
- Visit the root node and print data of that node.
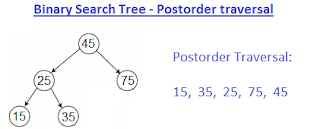 |
| Postorder traversal of binary tree example |
Detailed explanation on Postorder traversal: Postorder traversal of binary tree
Breadth First Traversal
Breadth First Traversal is a traversing way where child at same levels are read first before visiting their child. which is nothing but a Level order Traversal.
Levelorder traversal: To traverse a binary tree in Level order, following operations are carried-out
- Visit the nodes of tree Level by level (ie, from left to right, level by level).
- Here every Node of same Level is visited first before going to a lower levels.
45 25 75 15 35
For reading a Tree Level by Level, we require a Queue to store the Nodes.
Approach 1:
- Put a Root Node in a Queue.
- Iterate till the Queue is not Empty.
- While iterating, take one element from Queue say 45 in our example, print it and put children's of 45 in queue.
- Repeat steps till Queue is not empty.
 |
| Level order traversal using queue |
Approach 2:
If we know how to print all nodes at given level, then we can just find the height of the tree first and loop through the height of tree calling printAllNodesAtGivenLevel(i) where i goes from 0 to height of tree.
Java Program for Binary Tree Traversals.
package javabypatel.tree;
public class Node{
private int data;
private Node left;
private Node right;
public Node(int data) {
this.data=data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
BinaryTreeTraversal.java
package javabypatel.tree;
import java.util.LinkedList;
import java.util.Queue;
public class BinaryTreeTraversal {
private Node rootNode;
public static void main(String[] args) {
new BinaryTreeTraversal();
}
public BinaryTreeTraversal(){
addNode(rootNode, 45);
addNode(rootNode, 25);
addNode(rootNode, 75);
addNode(rootNode, 15);
addNode(rootNode, 35);
System.out.println("In Order Traversal :");
printTreeInOrder(rootNode);
System.out.println("\nPre Order Traversal :");
printTreePreOrder(rootNode);
System.out.println("\nPost Order Traversal :");
printTreePostOrder(rootNode);
System.out.println("\nLevel Order Traversal :");
printTreeLevelOrder(rootNode);
}
//Levelorder Printing.
private void printTreeLevelOrder(Node rootNode){
if(rootNode==null)
return;
Queue<Node> queue = new LinkedList<Node>();
queue.add(rootNode);
while(!queue.isEmpty()){
Node obj = (Node)queue.poll();
System.out.print(obj.getData() + " ");
if(obj.getLeft()!=null)
queue.add(obj.getLeft());
if(obj.getRight()!=null)
queue.add(obj.getRight());
}
}
//Inorder Printing.
private void printTreeInOrder(Node rootNode){
if(rootNode==null)
return;
printTreeInOrder(rootNode.getLeft());
System.out.print(rootNode.getData() + " ");
printTreeInOrder(rootNode.getRight());
}
//Preorder Printing.
private void printTreePreOrder(Node rootNode){
if(rootNode==null)
return;
System.out.print(rootNode.getData() + " ");
printTreePreOrder(rootNode.getLeft());
printTreePreOrder(rootNode.getRight());
}
//Postorder Printing.
private void printTreePostOrder(Node rootNode){
if(rootNode==null)
return;
printTreePostOrder(rootNode.getLeft());
printTreePostOrder(rootNode.getRight());
System.out.print(rootNode.getData() + " ");
}
private void addNode(Node rootNode, int data){
if(rootNode==null){
Node temp1 = new Node(data);
this.rootNode=temp1;
}else{
addNodeInProperPlace(rootNode, data);
}
}
private void addNodeInProperPlace(Node rootNode, int data){
if(data>rootNode.getData()){
if(rootNode.getRight()!=null){
addNode(rootNode.getRight(), data);
}else{
Node temp1 = new Node(data);
rootNode.setRight(temp1);
}
}else if(data<rootNode.getData()){
if(rootNode.getLeft()!=null){
addNode(rootNode.getLeft(), data);
}else{
Node temp1 = new Node(data);
rootNode.setLeft(temp1);
}
}
}
}
Print Nodes in Top View of Binary Tree
Print Nodes in Bottom View of Binary Tree.
Print a Binary Tree in Vertical Order
Zig Zag Traversal of Binary Tree.
Boundary Traversal of binary tree.
Enjoy !!!!
If you find any issue in post or face any error while implementing, Please comment.










Post a Comment