How to add a Node in Binary Tree and not a Binary Search Tree?
To add a Node in a Binary Tree, Let us first fix our protocol of how we are going a insert a node in Binary Tree.
Before going further, I would like to clear the difference between Binary Tree and Binary Search Tree, you are welcome to skip this part if you are already aware of,
Binary Tree: A tree is called Binary Tree if each node of tree has no more than 2 child node.
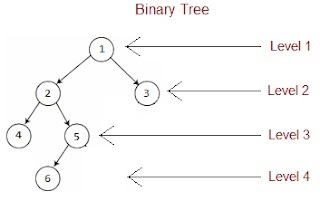 |
| Binary Tree Example |
- pre order traversal of binary tree in java
- post order traversal of binary tree in java
- in order traversal of binary tree in java
- level order traversal of binary tree using queue in java
- zigzag traversal of binary tree
- reverse level order traversal of binary tree
- boundary traversal of binary tree
- vertical traversal of binary tree
Binary Search Tree: It is a special type of Binary Tree where it follow below rules,
So to add a node, we will start scanning a Binary Tree level by level and wherever we encounter a Node which has no child node or has only one child node, that would be our target node to insert a new Node
See below image to get better understanding of position of a new Node to insert. Given a binary tree, we need to add a Node with value 8 marked in dotted lines below in its correct position.
- Nodes on left subtree must have value less than the parent node.
- Nodes on right subtree must have value greater than the parent node.
 |
| Sample Binary Search Tree |
How to add a Node in Binary Tree:
For adding a node in Binary tree we just need to make sure we are not breaking the rule of Binary tree that is, "each node of tree has no more than 2 child node".So to add a node, we will start scanning a Binary Tree level by level and wherever we encounter a Node which has no child node or has only one child node, that would be our target node to insert a new Node
See below image to get better understanding of position of a new Node to insert. Given a binary tree, we need to add a Node with value 8 marked in dotted lines below in its correct position.
 |
| Add a node in binary tree |
Java Program to insert a Node in Binary Tree and not a Binary Search Tree?
package javabypatel;
import java.util.LinkedList;
import java.util.Queue;
public class AddNodeInBinaryTree {
private Node rootNode;
public static void main(String[] args) {
new AddNodeInBinaryTree();
}
public AddNodeInBinaryTree(){
addNodeInBinaryTree(rootNode, 1);
addNodeInBinaryTree(rootNode, 2);
addNodeInBinaryTree(rootNode, 3);
addNodeInBinaryTree(rootNode, 4);
addNodeInBinaryTree(rootNode, 5);
printTreeLevelOrder(rootNode);
}
//Iterative way of adding new Node in Binary Tree.
private void addNodeInBinaryTree(Node rootNode, int data){
if(rootNode==null){
// No Nodes are Present, create one and assign it to rootNode
this.rootNode = new Node(data);
}else{
//Nodes present, So checking vacant position for adding new Node in sequential fashion
//Start scanning all Levels (level by level) of a tree one by one until we found a node whose either left or right node is null.
//For each and every node, we need to check whether Left and Right Node exist?
//If exist, then that node is not useful for adding new node but we need to store left and right node of that node for later processing
//that is why it is stored in Queue for sequential placement.
//If not exist, then we found a node, where new node will be placed but not sure on left or right, so check which side is null and place new node there.
Queue<Node> q = new LinkedList<Node>();
q.add(rootNode);
while(!q.isEmpty()){
Node node = q.poll();
if(node.getLeft()!=null && node.getRight()!=null){
q.add(node.getLeft());
q.add(node.getRight());
}else{
if(node.getLeft()==null){
node.setLeft(new Node(data));
}else{
node.setRight(new Node(data));
}
break;
}
}
}
}
private void printTreeLevelOrder(Node rootNode) {
if(rootNode==null)
return;
Queue<Node> q = new LinkedList<Node>();
q.add(rootNode);
while(!q.isEmpty()){
Node node = q.poll();
System.out.print(node.getData() + " ");
if(node.getLeft()!=null)
q.add(node.getLeft());
if(node.getRight()!=null)
q.add(node.getRight());
}
}
}
Top Binary Tree Interview Questions.
Binary Tree Traversals - Inorder, Preorder, Postorder, Levelorder
Delete a node in Binary Search Tree.
Check a given two Binary Trees are Mirror Image of each other.
Construct a Binary Tree from In-order and Post-order traversals.
ZigZag Traversal of Binary Tree.
Types of Binary Tree
Enjoy !!!!
If you find any issue in post or face any error while implementing, Please comment.










Post a Comment