Delete a node in Binary Search Tree in Java

How to delete a Node in Binary Search Tree in Java?

Let's see how to delete a node in binary search tree with example and java program.

There are 3 cases that need to be considered while deleting a node from Binary Search Tree.

Node to delete has no children that is no left child and no right child present. Case 1 in below image.
Node to delete has only one child either left child or right child present. Case 2 in below image.
Node to delete has both child that is left child and right child present. Case 3 in below image.

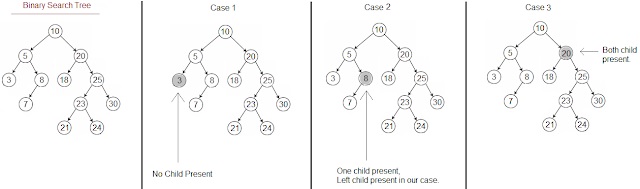Delete a node in binary search tree cases

Binary Search tree Deletion Algorithm

Case 1: Node to delete has No child node.
For case 1, it is very much straightforward,

Search for the node that need to be deleted.
Node to be deleted is either on left side or on right side of its parent node.
If node to be deleted is on left side of its parent node then mark Left side of parent node to null. Eg: parent.setLeft(null);
If node to be deleted is on right side of its parent node then mark Right side of parent node to null. Eg: parent.setRight(null);

Case 1 - Delete leaf node in binary search tree

Case 2: Node to delete has one child node either Left or Right node present.
For case 2, it is very much straightforward,

Search for the node that need to be deleted.
Node to be deleted is either on left side or on right side of its parent node.
Node to be deleted has only child present that can be on left side or right side.
If node to be deleted has left child present, then directly connect its parent node to left child node of node to be deleted. Eg: parent.setLeft(child.getLeft());
If node to be deleted has right child present, then directly connect its parent node to right child node of node to be deleted. Eg: parent.setRight(child.getRight());
In this way node to be deleted will be removed from the Tree and parent node will be directly connected to child node of node to be deleted.

Case 2 - Delete node in binary search tree

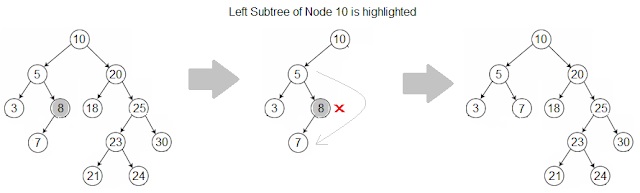
Case 3: Node to delete has both child present
For case 3, it is little bit tricky

Search for the node that need to be deleted.
Now, instead of deleting the node, we will replace the data of node to be deleted with the data that will be best fit in that place.
Which data will be best fit? Search the data from the sub tree of node to be deleted and find the node whose data when placed at the place of node to be deleted will keep the Binary Search Tree property(key in each node must be greater than all keys stored in the left sub-tree, and smaller than all keys in right sub-tree) intact.
Find minimum element from the right sub tree of node to be deleted or find maximum element from the left sub tree of node to be deleted and copy that Node data to the data of node to be deleted.
Delete the node which we found the best fit in step 5.

Case 3 - Binary search tree deletion algorithm

Java Program to delete a Node in BST (Binary Search Tree).

package javabypatel;

public class DeleteNodeInBinarySearchTree {
 private Node rootNode;

 public static void main(String[] args) {
  new DeleteNodeInBinarySearchTree();
 }

 public DeleteNodeInBinarySearchTree(){

  addNode(rootNode, 10); 
  addNode(rootNode, 5); 
  addNode(rootNode, 20); 
  addNode(rootNode, 3); 
  addNode(rootNode, 8); 
  addNode(rootNode, 18); 
  addNode(rootNode, 25); 
  addNode(rootNode, 7); 
  addNode(rootNode, 23); 
  addNode(rootNode, 30); 
  addNode(rootNode, 21); 
  addNode(rootNode, 24); 

  printTreeInOrder(rootNode);

  rootNode = deleteNode(rootNode,20);

  printTreeInOrder(rootNode);
 }


 private Node deleteNode(Node rootNode, int data) {
  if(rootNode==null){
   return null;
  }

  if(data==rootNode.getData()){

   if(rootNode.getLeft()!=null && rootNode.getRight()!=null){
    
    //Find Minimum from Right Tree OR find Maximum from Left Tree.
    Node minNode = getMinimumNodeFromRight(rootNode.getRight());
    rootNode.setData(minNode.getData());

    rootNode.setRight(deleteNode(rootNode.getRight(), minNode.getData()));
    System.out.println(minNode);
   
   }else if(rootNode.getLeft()==null){
    return rootNode.getRight();
   }else{
    return rootNode.getLeft();
   }

  }else if(data>rootNode.getData()){
   rootNode.setRight(deleteNode(rootNode.getRight(), data));
  }else{
   rootNode.setLeft(deleteNode(rootNode.getLeft(), data));
  }

  return rootNode;
 }

 public Node getMinimumNodeFromRight(Node node){
  if(node.getLeft()==null){
   return node;
  }else{
   Node n = getMinimumNodeFromRight(node.getLeft());
   return n;
  }
 }
   
 private void printTreeInOrder(Node rootNode){
  if(rootNode==null)
   return;
  printTreeInOrder(rootNode.getLeft());
  System.out.print(rootNode.getData() + " ");
  printTreeInOrder(rootNode.getRight());
 }

 private void addNode(Node rootNode, int data){
  if(rootNode==null){
   this.rootNode=new Node(data);
  }else{
   addNodeInProperPlace(rootNode, data);
  }
 }
 
 private void addNodeInProperPlace(Node rootNode, int data){ 
  if(data>rootNode.getData()){
   if(rootNode.getRight()!=null){
    addNode(rootNode.getRight(), data);
   }else{
    Node temp1 = new Node(data);
    rootNode.setRight(temp1);
   }
  }else{
   if(rootNode.getLeft()!=null){
    addNode(rootNode.getLeft(), data);
   }else{
    Node temp1 = new Node(data);
    rootNode.setLeft(temp1);
   }
  }
 }
 
}